本文为icourse哈工大课程《大数据算法》笔记
大数据算法概述
大数据4个V
- Volume:数据规模大
- Variet:数据类型多,多源异构
- Velocity:处理速度快
- Value:基于深度分析的新价值
大数据上问题求解计算问题的过程
- 先判断是否可以计算。一个普通数据量上都不能计算的问题,在大数据上,也不可计算
- 判断在现有的资源约束下,时间约束下,数据量下,是否是能行可计算
- 算法分析与设计
- 编程实现算法(Hadoop/Spark)
- 软件系统构造
大数据算法定义
在给定的资源约束下,以大数据为输入,在给定时间约束内可以生成满足给定约束结果的计算。
大数据算法可以不是
- 精确算法:很多情况下,在有限资源下,可以选择舍弃精度换时间
- 内存算法:难以在内存中存储全部数据,有时候考虑外存和多级存储器
- 串行算法:大数据可以考虑在多台机器上执行
- 仅在电子计算机上运行的算法:可以有人来参与到程序的执行
大数据不仅是:
- 云计算:大数据还可以在一些计算能力弱的平台上进行(如手机)
- MapReduce:除了并行模型,还有很多其他大数据的编程模型,如设计亚线性算法,或者引入人的参与
- 大数据分析与挖掘的算法:一些基础问题,例如排序于查找,在大数据环境下都需要重新设计
大数据中的两个特点Volume和Velocity决定了大数据算法的设计。我们希望扫描数据$O(n)$或者$O(logn)$时间来解决问题。
大数据算法设计难度
- 访问全部数据时间太长
- 读取部分数据(时间亚线性算法)
- 数据难以放入内存计算
- 将数据存储到磁盘(外存算法)
- 仅基于少量数据进行计算(空间亚线性算法)
- 单个计算机难以保存全部数据,计算需要整体数据
- 并行处理(并行算法)
- 计算机计算能力或者知识不足
- 人来参与(众包算法)
大数据算法设计技术
- 精确算法:大数据在精确计算上的应用
- 并行算法
- 近似算法:牺牲一部分精确性,在多项式时间内,给出精确性,并控制误差
- 随机算法:利用随机化的方法,进行抽样
- 在线算法/数据流算法:当数据源源不断时,在有限时间和空间内得到结果
- 外存算法:当数据无法存储在内存时
- 面向新型体系结构的算法:GPU大规模并行
- 现代优化算法:蚁群算法,模拟退火,进化算法
大数据算法分析
- 时间空间复杂性分析:和传统算法分析一致
- IO复杂性分析:大数据算法区别于传统内存算法,IO会直接影响算法性能
- 结果质量分析:(在得不到精确解时,要分析近似比;对于数据流算法,分析competitive radio,即知道整个数据集和只知道当前情况下,算法结果的区别)
- 通讯复杂性:区别于传统单机结构,大数据的多机并行执行涉及到通讯复杂性问题
亚线性算法
时间/空间/能量/通讯/IO消耗是:$o(输入规模)$
亚线性时间算法
- 亚线性时间近似算法
- 例:给一个社交网络,在不访问所有节点的情况下,求平均每个节点的度
- 性质检测算法
亚线性空间算法
- 面向源源不断的数据流
- 例:对一个几乎无限长的序列,不保存所有数字情况下,求中位数
水库抽样(空间亚线性算法)
输入:一组数据,大小未知
输出:这组数据的$k$个均匀抽样
要求:
- 仅扫描一次数据
- 空间复杂度$O(k)$,即:不能保存所有数据
- 扫描到数据前$n$个数字时候$(n>k)$,保存当前已扫描数据的$k$个均匀抽样
算法:
- 申请一个长度为$k$的数组$A$保存抽样
- 保存首先接收到的$k$个元素
- 当接收到第$i$个新元素的$t$时,以$k/i$的概率随机替换$A$中的元素(即:生成$[1,i]$间的随机数$j$,若$j \leq k$,则以$t$替换$A[j]$)
性质
该采样是均匀的
第$i$个数被第一次选中的概率是$\frac{k}{i}$,之后第$i+1$次中,第$i$个数依旧不会替换的概率是$(1- \frac{1}{i+1})$。依此类推,第$i$个数在第$n$个数到来后,依旧被保留在抽样中的概率是:它和$i$是无关的,即每个数字无论到来的次序,被保留的概率均等,所以采样是均匀的。
空间复杂度$O(k)$
平面图直径计算(时间亚线性算法)
输入:$m$个顶点的平面图,任意两点之间的距离存储在矩阵$D$中,即点到点的距离是$D_{ij}$
- 输入大小是:
- 最大的$D_{ij}$是图的直径
- 点之间的距离对称且满足三角不等式
输出:图的直径和距离最大的$D_{ij}$
要求:运行时间为$o(n)$,不能遍历所有数据
无法在要求的时间内得到精确解,寻找近似算法
近似算法:
- 任意选择$k \leq m$
- 选择使得$D_{kl}$最大的$l$
- 输出$D_{kl}$和$(k,l)$
该算法只访问了矩阵一行数据,显然不能精确计算结果,但是我们可以分析他的误差范围,假设$D_{ij}$是最优解,根据三角不等式:
又因为$D_{kl}$在矩阵$k$行/列中最大,所以
即
因此近似比2
运行时间
近似算法
- 什么是近似算法
- 近似算法是用来解决优化问题
- 能够给出优化问题的一个近似优化解的算法
- 近似算法解的近似度
- 问题每一个可能的解都具有一个代价
- 问题的优化解决可能具有最大或者最小代价
- 我们希望寻找问题的一个误差最小的近似优化解
- 我们需要分析近似解代价和优化解代价的差距
- Ratio Bound(近似比)
- 相对误差
- $(1+\epsilon)$-近似
Ratio Bound
设A是一个优化问题的近似算法,A具有Ratio Bound $p(n)$,如果
其中$n$是输入大小,$C$是A产生的近似解的代价,$C^{\ast}$是最优化解的代价。取$max$是为了应对最大化和最小化问题,使得结果$Ratio \text{总是} \geq 1$,$Ratio$越小越好。
- 最大化问题中,往往$C \leq C^{\ast}$,所以取$Ratio=\frac{C^{\ast}}{C}$
- 最小化问题中,往往$C \geq C^{\ast}$,所以取$Ratio=\frac{C}{C^{\ast}}$
相对误差
近似算法的相对误差定义为:
相对误差界定义为:
全0数组判定(时间亚线性判定算法)
输入:包含$n$个元素的0,1数组$A$
输出:$A$中的元素是否全是0
要求:运行时间为$o(n)$
判定问题的近似求解
- 输入满足某种性质或者远非满足此性质
判定问题的近似解的定义:输入满足某种性质或者远非满足此性质
$\epsilon$-远离
对于输入串$x$,如果从$x$到串的集合$L$中任意字符串的汉明距离至少为$\epsilon \vert x \vert$,则$x$是$\epsilon$-远离$L$的
在信息理论中,Hamming Distance 表示两个等长字符串在对应位置上不同字符的数目
算法描述
- 在$A$中随机独立抽取$s=\frac{2}{\epsilon}$个位置上的元素
- 检查抽样,若不包含1则输出“是”,否则输出“否”
精确性分析
- 如果$A$是全0数组,始终输出“是”
- 如果A是$\epsilon$-远离的,此时每位数为1的概率是$\epsilon$,不为1的概率是$1-\epsilon$。可以得到出错的概率小于$\frac{1}{3}$:
运行时间$O(s)$
证据引理
如果一次测试以大于等于$p$的概率获得一个证据,那么$s=\frac{2}{p}$轮测试得到的证据概率大于等于$\frac{2}{3}$
对于一个判定问题$L$,其查询复杂性$q(n)$和近似参数$\epsilon$的性质测试算法是一个随机算法,其满足对于给定$L$的是一个实例$x$,最多进行$q(\vert x \vert)$次查询,并满足下述性质:
- 如果$x$在$L$中,该算法最少$\frac {2} {3}$的概率返回“是”
- 如果$x$是$\epsilon$-远离L的,该算法以最少$\frac {2} {3}$的概率返回“否”
亚线性算法例析
数据流中频繁元素(空间亚线性)
数据流模型
- 数据是流动的,只能顺序的扫描一次或几次,复杂度不超过$O(n)$,需要能快速处理新到来的元素
- 数据可能是无限的,内存有限的。内存通常取$O(log^{k}n)$或$O(n^{\alpha}) \ \forall\alpha \lt 1$
- 希望维护一个中间内存结果(概要)来给出相关性质的一个有效估计
- 数据流模型适用于大数据(顺序扫描数据仅一次,内存亚线性)
数据流常见运算
常见的求数据流的$min$,$max$,$sum$通过比较大小和累加可以只借由一个寄存器$s$实现。此处的“概要”$s$是可以合并的:多个流放到不同的$s$里,最后可以通过比较$s$大小或求和合并。
频繁元素求解问题
问题:给出一个序列$L = x_1,x_2,…$,求出现最多次的元素。令:
- $m$:数据流中元素个数
- $n$:不同元素数量
频繁元素求解在搜索引擎优化问题中有广泛应用。求解该种问题基于一个假设:
Zipf原则:典型的频率分布是高度倾斜的,只有少数元素是频繁元素。
精确解:每个元素设置计数器,处理每个元素时增加对应元素的计数器。当内存只能提供$k$个计数器,$k << n$,问题就来了。
近似算法(MG算法):
Misra Gries算法:
处理每个收到的元素$x$:
- 如果已经给$x$分配了计数器,增加计数
- 如果没有给$x$分配计数器,但计数器个数小于$k$,为$x$分配计数器,并设为1
- 否则,所有计数器减1,删除值为0的计数器
为了防止计数器减少导致的频繁元素出现次数计数减少,计:
- 整个结构的权重(计数器的和)记作$m^{\prime}$
- 整个数据流的权重(全部元素的数量)是$m$
- 每次计数器降低会减少$k$个计数,然后新输入元素此次出现,实际上少计入了$k+1$次元素,所以最多有$\frac{m-m^{\prime}}{k+1}$轮减少计数
即:估计值与真实值差最多是$\frac{m-m^{\prime}}{k+1}$,当数据流中元素总数远大于$\frac{m-m^{\prime}}{k+1}$,得到一个好的估计。
错误的界限和$k$成反比。计算时,可以记录$m$和$m^{\prime}$,然后估算出与真实值的误差。由于$zipf$原则,该算法长期有效。
最小生成树计数(时间亚线性的计算问题)
一般的求最小生成树的算法(贪心算法)是复杂度为$mlog(n)$的prime和kruskal算法,而大数据业务中尽可能实现线性或亚线性算法。
输入:无向有权联通图$G=(V,E)$,其顶点的度最大为$D$,边上的权来自整数集合$\lbrace 1,2,\dots,w \rbrace$
输出:图$G$的最小生成树的权重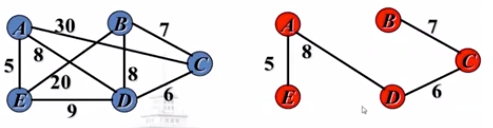
可以利用特定子图联通分量的数量估计最小生成树的权重。假设所有边权重都是1或2,最小生成树的权重可以表示为
其中$\sharp N_i$是最小生成树中权重至少为$i$的的边的数量。因为最小生成树是连通图,$\sharp N_1$等于最小生成树边的数量,等于$n-1$,即:
如果把权重为2的边都去掉,最小生成树会变成由权重为1的边构成的若干个连通分量(单个节点也算一个连通分量),即:
对于一般情况:
- $G_i$:$G$中包含所有权重小于等于$i$的边的子图
- $C_i$:$G_i$中连通分量的个数
- 最小生成树权重大于$i$的边数为$C_i-1$
即:$\sharp_i$=最小生成树权重大于$i$的边数=图$G$中包含权重小于等于$i$的边的子图中的联通分量的个数-1
因此,最小生成树(Minimal Spanning Tree)的权重(weight)应该是:
证明:
令$\betai$为MST中权重大于$i$的边的个数,显然:每一条MST的边对$W{MST}$的贡献为1,每个权重为$i(i \gt 1)$的边额外贡献了$i-1$。即:
所以要近似计算$W_{MST}$,只需要估算$c_i$:
基础算法:联通分量个数的估计
- 输入:图$G=(V,E)$,有$n$个顶点,表示为邻接矩阵,节点最大度为$d$
- 输出:联通分量个数
- 精确解时间复杂性:$\Omega(dn)$
算法:利用随机化方法,估计联通分量个数$\sharp CC$
- $\sharp CC \pm \epsilon n$的概率$\ge \frac{2}{3}$
- 运行时间和$n$无关
思路:
- 设$C$为连通分量个数
- 对于每个节点$u$,$n_u$表示$u$所在的连通分量节点数
- 对于每个联通分量$A$,$\Sigma_{u \in A} \frac{1}{n_u} = 1$
- 故对于整个图$V$,有:$\Sigma_{u \in V} \frac{1}{n_u} = C$
- 通过估计抽样顶点的$n_u$来估计这个和$C$
- 如果$u$所在的联通分量很小,其规模可以通过BFS估计
- 如果$u$所在的连通分量很大,$\frac{1}{n_u}$很小,对和$C$的贡献很小
- 可以在几步内完成BFS
- 令$\hat n_u = min \lbrace n_u, \frac {2}{\epsilon} \rbrace$
- 当节点数$n_u$小于$\frac {2}{\epsilon}$,$\hat n_u = n_u$
- 否则,$\hat n_u = \frac {2}{\epsilon}$,因此$0 \lt \frac {1}{\hat n_u} - \frac {1}{n_u} \lt \frac{1}{\hat n_u} = \frac{\epsilon}{2}$
- 在这种情况下,对$C$的估计
- 则$\vert C^{\prime} - C \vert = \vert \Sigma(\frac{1}{\hat n_u} - \frac{1}{n_u}) \vert \lt \frac {n \epsilon}{2}$
估计联通分量个数的伪码:
该算法循环$\frac{1}{\epsilon^2}$次,每次循环最多执行$\frac{2}{\epsilon}$次(做BFS),然后还是维护$L$的有序性,需要用到一个平衡二叉树来保持$L$。所以运行时间为$O(\frac{d}{\epsilon^3} log \frac {1}{\epsilon})$
接下来分析抽样和遍历每个点精确求BFS的结果查大于$\frac{\epsilon n}{2}$概率是小于$\frac{1}{3}$的,即:
来说明估计值和真实值相差过大的概率很小。
- 对于采样种的第$i$个节点$u$,令$Y_i = \frac {1} {\hat n_u}$
- $Y=\Sigma_{i=1}^s Y_i = \frac {s \bar{C}}{n}$
- $E[Y] = \Sigma{i=1}^s E[Y_i] = sE[Y_1] = s \times \frac{1}{n} \Sigma{u \in V} \frac{1}{\hat{n_v}} = \frac{s \hat C}{n}$
Hoeffding界:
$Y1,Y_2\dots Y_s$为$[0,1]$区间内独立同分布的随机变量,令$Y=\Sigma{i=1}^{s} Y_i$,则$Pr[\vert Y - E[Y] \vert \geq \delta] \leq 2e^{\frac {-2\delta^{2}}{s}}$
因此,下列事件发生的概率大于$\frac {2}{3}$:
综上所述,有$n$个顶点的图中,若其顶点的度至多为$d$,则其连通分量的估计误差最多为$\pm \epsilon n$
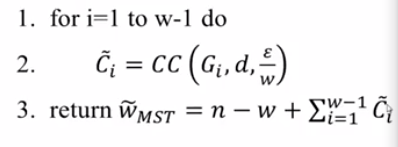
分析:
- 假设$C_i$的估计都是正确的,$\vert \bar{C_i} - C_i \vert \leq \frac{\epsilon}{w} n$,则
- $Pr[所有w-次估计都正确] \geq (\frac{2}{3})^{w-1}$
- 这还不够好,可以通过CC算法,取合适的$s$值,使每一轮的错误概率$\leq \frac{1}{3w}$,应当取多少
乘近似:
- 对于MST的代价,可以从加的近似导出乘法的近似
- $\epsilon n$加近似
- $(1 \pm 2\epsilon)$乘近似
序列有序的判定(时间亚线性算法的判定问题)
输入:$n$个数的数组,$x_1,x_2,\dots,x_n$
输出:这个数组是否有序?
常规算法需要访问$n$个数,时间复杂度$\Omega(n)$